Fractional part
All real numbers can be written in the form n + r where n is an integer (the integer part) and the remaining fractional part r is a nonnegative real number less than one. For a positive number written in decimal notation, the fractional part corresponds to the digits appearing after the decimal point.
The fractional part of a real number x is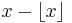 
, where 
is the floor function. It is sometimes denoted 
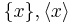or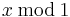 
.
If x is rational, then the fractional part of x can be expressed in the form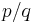 
, where p and q are integers and 
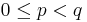; hence, the fractional part will always be less than 1. For example, if 
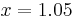, then the fractional part of x is .05 and can be expressed as 5/100 = 1/20.